Giới thiệu:
hello hello hello, mình là Doanh đây….
Bài viết này dành cho:
- Mọi người.
IoU là gì?
IoU viết tắt của Intersection over Union, IoU được sử dụng trong việc đánh giá tỉ lệ 2 khu vực trùng lặp lên nhau, đặc biệt được sử dụng ở các mô hình phát hiện vật thể như R-CNN, Faster R-CNN, YOLO,…
Thuật toán IoU tính toán dựa vào tọa độ 2 hình chữ nhật trong hệ tọa độ Descartes. Công thức IoU được tính bằng diện tích phần giao nhau chia cho diện tích phần hợp nhau, như hình bên dưới:
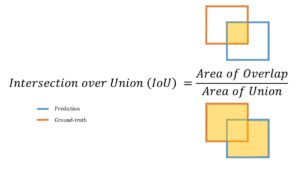
- Area of Overlap: là diện tích giao nhau giữa 2 hộp.
- Area of Union: là diện tích phần hợp nhau của 2 hộp.
Tính IoU:
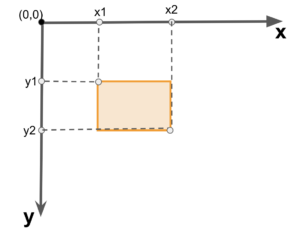
Ví dụ trong hệ tọa độ oxy, chúng ta có 2 hình chữ nhật A và B, với 2 điểm trên hệ tọa độ thì ta có thể xác định được 1 hình chữ nhật:
- Hình A được xác định bỡi 2 điểm: A_max(x1, y1) và A_min(x2, y2), với A_max là điểm phía trên bên trái, và A_min là điểm phía dưới bên phải. Điểm A được viết gọn lại thành 1 vector A(x1, y1, x2, y2).
- Tương tự như hình A, chúng ta có hình B(x’1, y’1, x’2, y’2).
Giờ ta bắt đầu tìm IoU của hình chữ nhật A và hình chữ nhật B:
Tính Area of Overlap, để tính diện tích phần giao nhau của 2 hình chữ nhật ta cần tìm tọa độ của phần giao nhau:
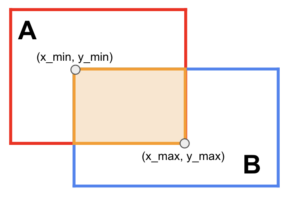
Để tính theo hệ tọa độ, ta tìm vùng giao giữa 2 hình chữ nhật:
x_1 = max ( A [ 0 ] , B [ 0 ]) y_1 = max ( A [ 1 ] , B [ 1 ]) x_2 = min ( A [ 2 ] , B [ 2 ]) y_2 = min ( A [ 3 ] , B [ 3 ])
Tính diện tích phần giao nhau:
inter = max( 0 , x_2 - x_1 ) * max( 0 , y_2 - y_1 )
Tính Area of Union, diện tích phần hợp nhau, là diện tích của cả 2 hình chữ nhật và trừ đi diện tích của phần giao nhau:
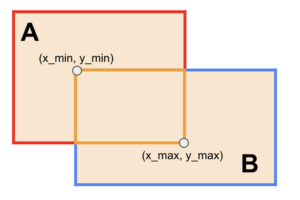
w1, h1 = A[2] - A[0], A[3] - A[1] w2, h2 = B[2] - B[0], B[3] - B[1] AArea = w1 * h1 BArea = w2 * h2 union = AArea + BArea - inter
Tính IoU, IoU được tính bằng tỉ lệ giữa phần giao, chia cho phần hợp.
iou = inter/union
Demo chạy code:
Hàm tính IoU:
def iou(A, B):
"""Returns Intersection over Union (IoU) of A(x1, y1, x2, y2) to B(x'1, y'1, x'2, y'2)
Args:
A (list): bbox of A
B (list): bbox of B
Returns:
float: IoU
"""
x_1 = max ( A [ 0 ] , B [ 0 ])
y_1 = max ( A [ 1 ] , B [ 1 ])
x_2 = min ( A [ 2 ] , B [ 2 ])
y_2 = min ( A [ 3 ] , B [ 3 ])
inter = max( 0 , x_2 - x_1 ) * max( 0 , y_2 - y_1 )
w1, h1 = A[2] - A[0], A[3] - A[1]
w2, h2 = B[2] - B[0], B[3] - B[1]
AArea = w1 * h1
BArea = w2 * h2
union = AArea + BArea - inter
iou = inter/union
return iou
Sử dụng để tính IoU:
A = [39, 63, 203, 112] B = [54, 66, 198, 114] print(iou(A, B)) #0.7957712638154734 A = [31, 69, 201, 125] B = [18, 63, 235, 135] print(iou(A, B)) #0.6093189964157706
Tổng kết:
IoU là một cách để đánh giá tỉ lệ trùng lặp giữa 2 hình chữ nhật với nhau trong hệ tọa độ Descartes. IoU được sử dụng trong các mô hình phát hiện vật thể để tính tỉ lệ trùng lặp giữa bounding box được label và bounding box được mô hình dự đoán ra. Ở phần sau, chúng ta cùng sử dụng IoU trong YOLO nhé.
Tài liệu tham khảo:
[1] https://github.com/ultralytics/yolov5/blob/master/utils/metrics.py#L216
[2] https://github.com/pjreddie/darknet/blob/a3714d0a2bf92c3dea84c4bea65b2b0c64dbc6b1/src/box.c#L179
[3] https://pyimagesearch.com/2016/11/07/intersection-over-union-iou-for-object-detection/

