[Part 1] Constrained Optimization – Math Approach for Data Science

1. Giới thiệu về Continuous Optimization.

Lý thuyết tối ưu là một trong những nhánh nghiên cứu toán trọng yếu, thuộc lĩnh vực toán ứng dụng, ảnh hướng rất nhiều đến các lĩnh vực khoa học công nghệ và kinh tế xã hội nói chung và lĩnh vực machine learning nói riêng. Trong lĩnh vực nghiên cứu về lý thuyết tối ưu, hai nhánh chính được các nhà nghiên cứu quan tâm bao gồm lý thuyết tối ưu không ràng buộc (Unconstrained Optimization) và lý thuyết tối ưu có ràng buộc (Constrained Optimization).

Nội dung về Unconstrained Optimization xoay quanh về các thuật toán tối ưu như Gradient Descent và các biến thể của nó. Những khái niệm này đã được giới thiệu chi tiết trên khắp các diễn đàn khác nhau, bạn đọc có thể tìm đọc thêm ở các trang blog sau:

Trong bài post này, ta chỉ quan tâm đến các vấn đề xoay quanh nội dung về Constrained Optimization. Để thuận tiện cho việc mô tả các khái niệm, định nghĩa, ta giả định các hàm mục tiêu đều khả vi và liên tục trên $\mathbb{R}^n$ .Dưới đây là mind map về các vấn đề Continuous Optimization liên quan đến Machine Learning.

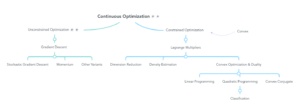
2. Constrained Optimization.

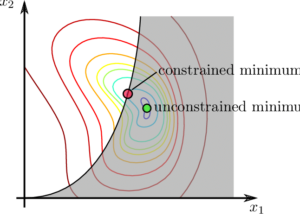
Các bài toán về tối ưu không ràng buộc mô tả vấn đề tìm cực tiểu của hàm số

$min f(x)$

với $f: \mathbb{R}^D \rightarrow \mathbb{R}$

Trong nội dung này, chúng ta sẽ có thêm những điều kiện rằng buộc là những hàm thực $g_i : \mathbb{R}^D \rightarrow \mathbb{R}$ với $i = 1,...,m$ . Lúc này, bài toán tối ưu của chúng ta trở thành:

$min f(x)$ (1)

subject to $g_i (x) \leq 0$ với mọi $i = 1,...,m$ .

Ở đây, điều đáng lưu ý là hàm $f$ và $g_i$ có thể là hàm non-convex (không lồi). Các vấn đề liên quan đến hàm lồi sẽ được giới thiệu trong bài viết tiếp theo của series. Ta có thể thấy rằng, việc chuyển đổi từ bài toán có ràng buộc (1) thành bài toán không ràng buộc sẽ thông qua hàm chỉ thị (indicator function) mô tả dưới đây:

$J(x) = f(x) + \sum\limits_{i = 1}^m {{1(g_i (x))}},$ (2)

Trong đó $1(z)$ là hàm vô hạn bước (infinite step function) (3) :

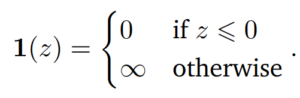
Hàm này sẽ phạt vô hạn nếu ràng buộc của bài toán không được thỏa mãn, do đó ta có thể đưa từ bài toán không ràng buộc về bài toán có ràng buộc. Tuy nhiên, hàm vô hạn bước cũng sẽ gặp khó khăn trong việc tối ưu. Chính vì vậy, Lagrange Multipliers ra đời để giải quyết cho khó khăn này. Ý tưởng chính của Lagrange multipliers (Nhân tử Lagrange) là thay thế hàm bước (step function) bằng hàm tuyến tính (linear function).

3. Lagrange Multipliers và bài toán đối ngẫu.

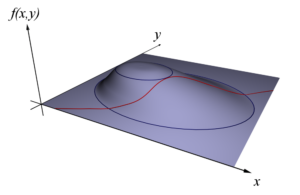
Chúng ta liên hệ với bài toán ràng buộc (1) qua việc sử dụng Lagrange multipliers với $\lambda_i \geq 0$ lần lượt tương ứng cho các bất đẳng thức ràng buộc $g_i(x)$ . Ta có (4):

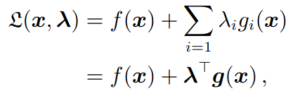
Trong đó, ta concatenate tất cả ràng buộc $g_i (x)$ thành vector $g(x)$ , và tất cả Lagrange multipliers thành vector $\lambda \in \mathbb{R}^m$ . Bài toán lúc này chúng ta cần giải quyết là Lagrangian duality (Bài toán đối ngẫu Langrange). Thông thường, ý tưởng để giải quyết bài toán tối ưu đối ngẫu sẽ đưa bài toán gốc (primal) thành bài toán quy hoạch tuyến tính khác, gọi là bài toán đối ngẫu (duality). Ở đây, chúng ta sẽ giới thiệu cách tiếp cận để giải quyết bài toán đối ngẫu: Lagrangian Duality. Ở bài viết tiếp theo sẽ giới thiệu cách tiếp cận giải quyết sử dụng Legendre-Fenchel Duality.

Trở lại bài toán (1), ta nói:

$min f(x)$

subject to $g_i (x) \leq 0$ với mọi $i = 1,...,m$ .

là bài toán gốc (primal problem), với các biến x gốc (prmial variables). Từ đó, bài toán đối ngẫu Lagrange sẽ được phát biểu như sau:

$max D(\lambda)$ (5)

subject to $\lambda \geq 0$

với $\lambda$ được gọi là biến đổi ngẫu và $D(\lambda) = min_{x \in \mathbb{R}^d} L(x, \lambda)$ .

Ta quan tâm đến 2 khái niệm độc lập được Boyd and Vandenberghe đưa ra khi giải quyết bài toán tối ưu không ràng buộc được giới thiệu trong kiến thức tối ưu lồi (Convex Optimization). Khái niệm thứ nhất là minimax inequality (bất đẳng thức tối thiếu hóa), được định nghĩa là với mọi hàm hai biến $\varphi (x,y)$ , maximin sẽ luôn nhỏ hơn minimax. (6)

Bất đẳng thức trên có thể được chứng minh thông qua việc đánh giá bất đẳng thức dưới đây. (7)

Trong đó, khi lấy max theo biến y bên vế trái sẽ giữ nguyên chiều bất đẳng thức vì bất đẳng thức luôn đúng với mọi y. Tương tự, ta lấy min theo biến x bên vế phải cũng sẽ không đổi chiều bất đẳng thức. Khi đó, ta chứng minh được (6) từ mệnh đề (7).

Khái niệm thứ hai là đối ngẫu yếu (weak duality), chỉ ra rằng giá trị gốc sẽ luôn lớn hơn hoặc bằng giá trị đối ngẫu. Biểu thức sẽ được mô tả chi tiết bên dưới. Lưu ý rằng, sự khác biệt giữa biểu thức (2) và Lagrangian ở biểu thức (4) là ta đã đưa hàm chỉ thị về hàm tuyến tính. Do đó, khi $\lambda \geq 0$ , giá trị Lagrangian $L(x, \lambda)$ là chặn dưới của $J(x)$ . Do đó, max của $L(x, \lambda)$ theo biến $\lambda$ được biểu diễn:

Lưu ý rằng, bài toán ban đầu cần giải quyết là tìm minimum của hàm $J(x)$ ,

Sử dụng bất đẳng thức minimax (6), ta biến đổi thứ tự minimum và maximum ở giá trị nhỏ hơn, ta được:

Đây được gọi là biểu thức đối ngẫu yếu (weak duality).

4. Cách biến đổi bài toán gốc thành bài toán đối ngẫu và các ví dụ.

Ví dụ 1: Đưa bài toán có ràng buộc đơn giản về bài toán không ràng buộc.

Như chúng ta đã biết ở trên, lý thuyết đối ngẫu được phát triển từ phương pháp nhân tử Lagrange, thường được sử dụng để tìm cực trị của một hàm với các ràng buộc đẳng thức. Chẳng hạn, để giải bài toán tối ưu có ràng buộc bên dưới:

$min x^2 + y^2$

với ràng buộc $x + y = 1$

Ta đặt nhân tử Lagrange $p$ và thiết lập hàm Lagrange $L(x, y, p)$ định bởi

$L(x, y, p) = x^2 + y^2 + p(1 - x - y)$

Với p được cố định, ta đi tìm giá trị nhỏ nhất của hàm Lagrange với x và y không có ràng buộc nào. Điều này được thực hiện bằng cách cho các đạo hàm riêng $\delta L / \delta x$ và $\delta L / \delta y$ bằng không. Phương án tối ưu của bài toán không ràng buộc này là

$x = y = \frac{p}{2}$

và phụ thuộc vào p. Ràng buộc $x + y = 1$ cho ta thêm hệ thức $p = 1$ , và phương án tối ưu của bài toán gốc là $x = y = \frac{1}{2}$ .

Ý tưởng chính trong ví dự trên như sau. Thay vì tuân thủ ràng buộc cứng

$x + y = 1$

ta cho phép ràng buộc này bị vi phạm và liên kết với một nhân tử Lagrange p (còn gọi là giá – price) với lượng vi phạm

$1 - x - y$

Điều này dẫn đến bài toán tìm giá trị nhỏ nhất không ràng buộc của

$x^2 + y^2 + p(1 - x - y)$

Khi giá được chọn một cách đúng đắn (p=1, trong ví dụ trên), phương án tối ưu cho bài toán có ràng buộc cũng là phương án tối ưu cho bài toán không ràng buộc. Cụ thể, với p = 1, sự có mặt hay vắng mặt của ràng buộc cứng x + y = 1 không ảnh hướng đến chi phí tối ưu.

Đối với quy hoạch tuyến tính, ta có tình trạng tương tự: ta liên kết một biến giá với mỗi ràng buộc và bắt đầu đi tìm các giá sao cho sự có mặt hay không có mặt của các ràng buộc không ảnh hướng đến chi phí tối ưu. Ta sẽ thấy rằng các giá này được xác định bằng cách giải quyết một bài toán quy hoạch tuyến tính mới, được gọi là đối ngẫu với bài toán gốc. Ví dụ bên dưới sẽ mô tả cách biến đổi từ bài toán gốc thành bài toán đối ngẫu.

Ví dụ 2: Phương pháp và ví dụ biến đổi bài toán đối ngẫu.

Xét bài toán quy hoạch tuyến tính gốc (primal) có phương án tối ưu là $x*$ :

$min c^T x,$

với ràng buộc $Ax=b,$

$x \geq 0.$

Với mỗi vector giá (price) $p \in \mathbb{R}^m$ , xét bài toán “nhẹ bớt” (relaxed):

$min c^T x +p^T (b - Ax),$

với ràng buộc $x \geq 0.$

Gọi $g(p)$ là chi phí tối ưu của bài toán “nhẹ bớt”. Ta có:

Khi đó, bài toán ban đầu trở thành:

Bài toán $max g(p)$ với p tự do, được gọi là bài toán đối ngẫu (dual) cần tìm. Kết quả chính của lý thuyết đối ngẫu bên trên khẳng định rằng chi phí tối ưu của bài toán đối ngẫu bằng với chi phí tối ưu của bài toán gốc.

Cho bài toán gốc với cấu trúc được chỉ ra như bên trái. Khi đó, bài toán đối ngẫu của nó có cấu trúc được chỉ ra như bên phải:

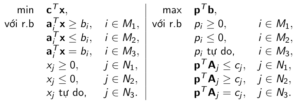
Với mỗi ràng buộc gốc (không phải ràng buộc về dấu của biến), ta đặt một biến đối ngẫu. Với mỗi biến gốc, ta đặt một ràng buộc đối ngẫu.

Ta có kết quả biến đổi đối ngẫu như sau:

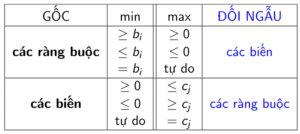
Dưới đây là minh họa của việc chuyển đổi từ bài toán gốc thành bài toán đối ngẫu:

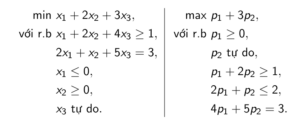
Mở rộng: Ta có định lý như sau. Nếu ta chuyển bài toán đối ngẫu thành bài toán giá trị nhỏ nhất tương đương rồi sau đó thiết lập bài toán đối ngẫu của nó, ta được một bài toán tương đương với bài toán gốc.

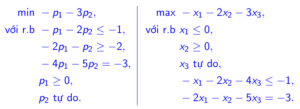
Kết luận: Chúng ta có thể thấy, ở bài toán tối ưu ban đầu là tối ưu có ràng buộc sẽ rất khó giải quyết. Tuy nhiên, biểu thức $min_{x \in \mathbb{R}^d} L(x, \lambda)$ là bài toán tối ưu không ràng buộc với giá trị cho trước là $\lambda$ . Nếu chỉ tiếp cận giải quyết bài toán tối ưu lồi, việc giải $min_{x \in \mathbb{R}^d} L(x, \lambda)$ sẽ dễ dàng. Ý tưởng chính của việc giải quyết bài toán Constrained Optimization là đưa về Unconstrained Optimization để giải quyết thông qua việc biến đổi từ bài toán gốc về bài toán đối ngẫu. Vấn đề còn lại chỉ là giải quyết Unconstrained Optimization – bài toán đã khá phổ biến với cách tiếp cận sử dụng Gradient Descent hoặc các thuật toán tối ưu tương tự. Ở bài viết tiếp theo, nội dung sẽ tập trung vào Convex Optimization (Tối ưu lồi).

P/s: Ở phần 1 này, nội dung kiến thức về nhân tử Lagrange, các lý thuyết về đối ngẫu và cách biến đổi là nền tảng quan trọng trong việc hiểu sâu hơn về bản chất các phương pháp giảm số chiều như PCA,… Ở phần tiếp theo, việc tìm hiểu các kiến thức về Convex Optimization sắp tới là nền tảng quan trọng trong việc nắm được bản chất toán học của bài toán phân loại Machine Learning như Support Vector Machine (Primal Support Vector Machine – Dual Support Vector Machine).

[Part 1] Constrained Optimization – Math Approach for Data Science

Fundamental of constrained optimization theory for deep understanding in machine learning

Data Scientist là nghề gì ?

Data Scientist sử dụng AirFlow

Huy Nguyen Thanh

Data Scientist sử dụng AirFlow

Leave a Reply Cancel reply